Macam-macam Algoritma Sorting dan Implementasi dengan PHP

Algoritma Sorting merupakan algoritma yang menempatkan elemen list pada urutan tertentu. Urutan yang paling sering digunakan ialah urutan numerikal dan urutan lexicographical. Sorting yang efisien sangat dibutuhkan untuk mengoptimisasi penggunaan dari algoritma lain seperti pencarian dan penggabungan yang membutuhkan list terurut untuk berjalan dengan sempurna, yang juga sering digunakan untuk Canonicalisisasi data dan menghasilkan output yang dapat dibaca manusia. (Wikipedia)

Sekarang masi Kita bahas satu-persatu :

1. Buble Sort
Merupakan algoritma pengurutan paling tua dengan metode pengurutan paling sederhana. Pengurutan yang dilakukan dengan membandingkan masing-masing item dalam suatu list secara berpasangan, menukar item jika diperlukan, dan mengulaginya sampai akhir list secara berurutan, sehingga tidak ada lagi item yang dapat ditukar.

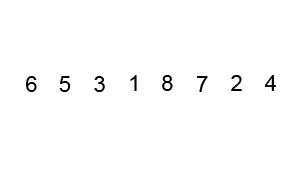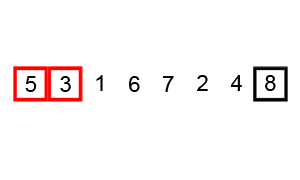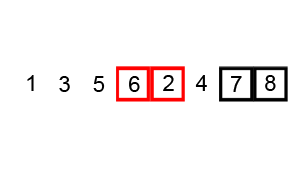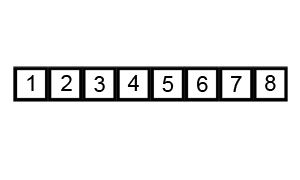
Implementasi :

echo "//bubble sortn";
$data=array(6,5,3,1,8,7,2,4);
function bubble_sort($data){
  $n=count($data);
  for ($i = 0;$i<$n;$i++){ for ($j = $n-1;$j>$i;$j--){
          if ($data[$j] < $data[$j-1]){ 
              $dummy=$data[$j];
              $data[$j]=$data[$j-1];
              $data[$j-1]=$dummy;
          }
      }    
  }
  return $data;
}
print_r(bubble_sort($data));

2. Insertion Sort
Algoritma insertion sort pada dasarnya memilah data yang akan diurutkan menjadi dua bagian, yang belum diurutkan dan yang sudah diurutkan. Elemen pertama diambil dari bagian array yang belum diurutkan dan kemudian diletakkan sesuai posisinya pada bagian lain dari array yang telah diurutkan. Langkah ini dilakukan secara berulang hingga tidak ada lagi elemen yang tersisa pada bagian array yang belum diurutkan.

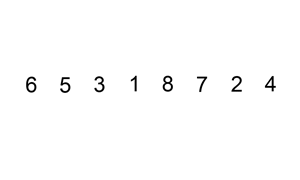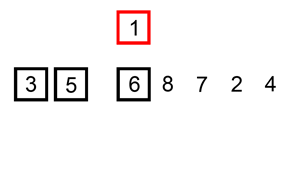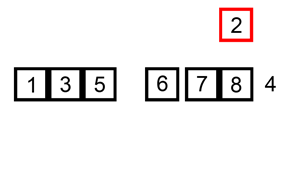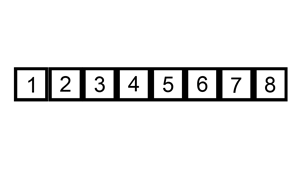
Implementasi :

echo "//insertion sortn";
$data=array(6,5,3,1,8,7,2,4);
function insertion_sort($data){
  $n=count($data);
  for ($i = 1;$i<$n;$i++){ for ($k = $i; $k>0; $k--) {
      if($data[$k]<$data[$k-1]){
        $dummy=$data[$k];
        $data[$k]=$data[$k-1];
        $data[$k-1]=$dummy;
      }
    }
  }
  return $data;
}
print_r(insertion_sort($data));

3. Selection Sort
Ide utama dari algoritma selection sort adalah memilih elemen dengan nilai paling rendah dan menukar elemen yang terpilih dengan elemen ke-i. Nilai dari i dimulai dari 1 ke n, dimana n adalah jumlah total elemen dikurangi 1.

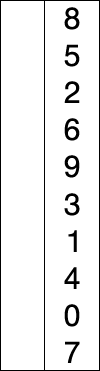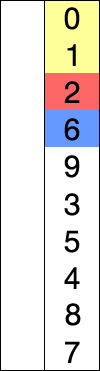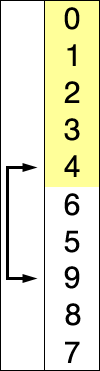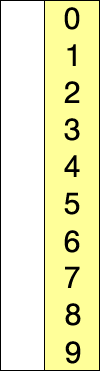
Implementasi :

echo "//selection sortn";
$data=array(6,5,3,1,8,7,2,4);
function selection_sort($data){
  $n=count($data);
  for ($i = 0;$i<$n;$i++){
    $k = $i;
    for ($j = $i+1;$j<$n;$j++){
      if ($data[$j] < $data[$k]) $k = $j;
    }   
    $dummy=$data[$i];
    $data[$i]=$data[$k];
    $data[$k]=$dummy;
  }
  return $data;
}
print_r(selection_sort($data));

4. Shell Sort
Merupakan algoritma yang stau jenis dengan insertion sort, dimana pada setiap nilai i dalam n/i item diurutkan. Pada setiap pergantian nilai, i dikurangi sampai 1 sebagai nilai terakhir.

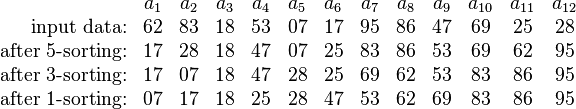
Implementasi :

echo "//shell sortn";
$data=array(6,5,3,1,8,7,2,4);
function shell_sort($data){
 $n=count($data);
   $k=0;
   $gap[0]=(int) ($n / 2);
   while($gap[$k]>1){
     $k++;
     $gap[$k]=(int)($gap[$k-1]/2);
   }
   for($i=0;$i<=$k;$i++){
   $step=$gap[$i];
     for($j=$step;$j<$n;$j++){
       $temp=$data[$j];
       $p=$j-$step;
       while($p>=0 && $temp<$data[$p]){
         $data[$p+$step]=$data[$p];
         $p=$p-$step;
       }
       $data[$p+$step]=$temp;
     }
   }
   return $data;
}
print_r(shell_sort($data));

5. Merge Sort
Algoritma dirumuskan dalam 3 langkah berpola divide-and-conquer. Berikut menjelaskan langkah kerja dari Merge sort.
- Divide : Memilah elemen – elemen dari rangkaian data menjadi dua bagian.
- Conquer : Conquer setiap bagian dengan memanggil prosedur merge sort secara rekursif
- Kombinasi : Mengkombinasikan dua bagian tersebut secara rekursif untuk mendapatkan rangkaian data berurutan

Proses rekursi berhenti jika mencapai elemen dasar. Hal ini terjadi bilamana bagian yang akan diurutkan menyisakan tepat satu elemen. Sisa pengurutan satu elemen tersebut menandakan bahwa bagian tersebut telah terurut sesuai rangkaian.

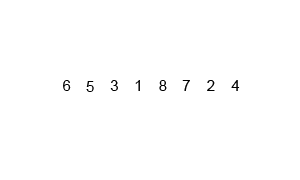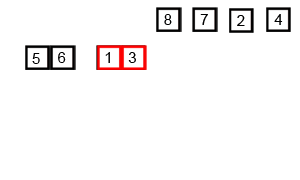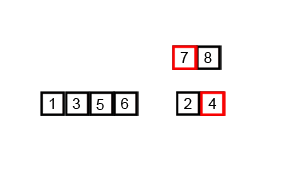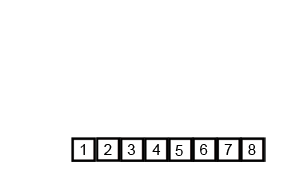
Implementasi :

echo "//merge sortn";
$data=array(6,5,3,1,8,7,2,4);
function merge_sort ($data){
  if (count($data) <= 1 ) return $data;
  $left  = merge_sort(array_splice($data,floor(count($data) / 2)));
  $right = merge_sort($data);
  $result = array();
  while (count($left) > 0 && count($right) > 0){
      if ($left[0] <= $right[0])
          array_push($result, array_shift($left));
      else
          array_push($result, array_shift($right));
  }
  while (count($left) > 0)
      array_push($result, array_shift($left));
  while (count($right) > 0)
      array_push($result, array_shift($right));  
  return $result;
}
print_r(merge_sort($data));

6. Quick Sort
Algoritma ini berdasar pada pola divide-and-conquer. Berbeda dengan merge sort, algoritma ini hanya mengikuti langkah – langkah sebagai berikut :

- Divide
Memilah rangkaian data menjadi dua sub-rangkaian A[p…q-1] dan A[q+1…r] dimana setiap elemen A[p…q-1] adalah kurang dari atau sama dengan A[q] dan setiap elemen pada A[q+1…r] adalah lebih besar atau sama dengan elemen pada A[q]. A[q] disebut sebagai elemen pivot. Perhitungan pada elemen q merupakan salah satu bagian dari prosedur pemisahan.

- Conquer
Mengurutkan elemen pada sub-rangkaian secara rekursif. Pada algoritma quicksort, langkah ”kombinasi” tidak di lakukan karena telah terjadi pengurutan elemen – elemen pada sub-array.

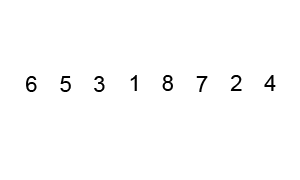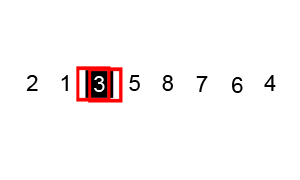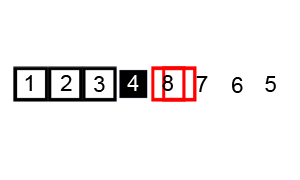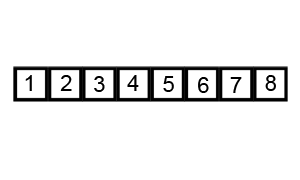
Implementasi :

echo "//quick sortn";
$data=array(6,5,3,1,8,7,2,4);
function quick_sort($data) {
    if(!count($data)) return $data;
    $pivot= $data[0];
    $low = $high = array();
    $n = count($data);
    for($i=1; $i < $n; $i++) {
        if($data[$i] <= $pivot) {
            $low [] = $data[$i];
        } else {
            $high[] = $data[$i];
        }
    }
    return array_merge(quick_sort($low), array($pivot), quick_sort($high));
}
print_r(quick_sort($data));

7. Heap Sort
Heap sort adalah sorting yang menggunakan struktur data heap, dengan nilai parent selalu lebih besar dari pada nilai childnya.

Algoritma :
- Buat suatu heap.
- Ambil isi dari root masukkan kedalam sebuah array.
- Hapus element root dengan mempertahankan properti heap.
- Ulangi sampai tree menjadi kosong

Implementasi :

echo "//heap sortn";
$data=array(6,5,3,1,8,7,2,4);
function build_heap(&$data, $i, $t){
  $tmp_var = $data[$i];    
  $j = $i * 2 + 1;
  while ($j <= $t)  {
   if($j < $t)
    if($data[$j] < $data[$j + 1]) {
     $j = $j + 1; 
    }
   if($tmp_var < $data[$j]) {
    $data[$i] = $data[$j];
    $i = $j;
    $j = 2 * $i + 1;
   } else {
    $j = $t + 1;
   }
  }
  $data[$i] = $tmp_var;
}

function heap_sort(&$data) {
  $init = (int)floor((count($data) - 1) / 2);
  for($i=$init; $i >= 0; $i--){
   $count = count($data) - 1;
   build_heap($data, $i, $count);
  }
  for ($i = (count($data) - 1); $i >= 1; $i--)  {
   $tmp_var = $data[0];
   $data[0] = $data[$i];
   $data[$i] = $tmp_var;
   build_heap($data, 0, $i - 1);
  }
}
heap_sort($data);
print_r($data);

Algoritma pembanding yang stabil menjaga urutan relatif dari rekord dengan indeks yang sama. (Indeks merupakan porsi dari rekors yang menjadi basis dari sorting; yang mungkin ataupun tidak termasuk dalam rekord tersebut.) Jika seluruh indeks berbeda maka perbedaan ini tidak dibutuhkan. Tetapi jika terdapat indeks yang sama, maka algoritma sorting itu stabil walaupun terdapat dua rekord (misalkan R dan S) dengan indeks yang sama, dan R muncul sebelum S pada list aslinya, kemudian R akan selalu muncul sebelum S pada list yang terurut. Ketika elemen yang sama tak dapat dibedakan, seperti dengan integer, atau secara umumnya, setiap data dimana seluruh elemen ialah nilai, tingkat kestabilannya tidak dipermasalahkan. Walaupun, asumsikan bahwa setiap angka yang ganda diurutkan berdasarkan komponen pertama mereka.